Recherche – activités récentes

Mon activité de recherche se déroule selon trois modalités : des travaux à caractère théorique ou fondamentaux, des conceptions et réalisations de logiciels et enfin, des applications notamment dans les domaines des Sciences Humaines et Sociales et la Santé.

Travaux théoriques

Graphes d’induction

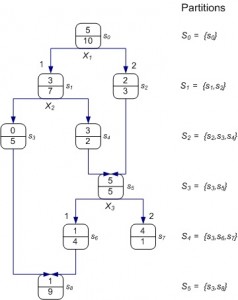
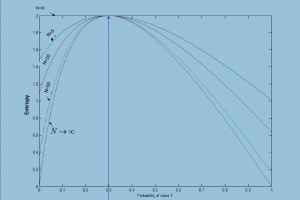
Les graphes d’induction dont les arbres de décision constituent une forme particulière. Dans le prolongement de mes travaux thèse (1985), j’ai proposé de nouveaux algorithmes d’induction de règles par des graphes latticiels et j’ai proposé une famille de mesures d’entropie sensibles aux effectifs. La raison est que les arbres de décision classiques se construisent par un processus de partitionnement récursif, conduisant le plus souvent à des sommets à faibles effectifs et, par conséquent, à des règles de décision peu fiables, donc à des modèles qui généralisent mal. La première réponse à ce problème a été apportée, au milieu des années 1980, par (Breiman et al.) avec les procédures d’élagage d’arbre.

Notre proposition d’introduire des structures latticielles, ainsi que de nouvelles mesures de partitionnement qui sont à la fois sensibles aux tailles d’échantillon et asymétriques, permet d’éviter ce sur-apprentissage qui nécessite un élagage. On peut ainsi voir cette contribution comme une sorte de pré-élagage par rapport au post-élagage proposé antérieurement.

Discrétisation

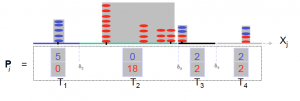
Le partitionnement récursif nécessite une discrétisation des attributs continus. Nous avons proposé de nouvelles approches qui prennent en compte différentes questions comme la complexité du découpage, l’estimation statistique des points de coupure les plus probables, etc. Cette discrétisation revient, d’une certaine manière, à réduire le nombre de branches possibles pour un graphe d’induction.  Dans le prolongement, on s’est posé la même question sur les variables qualitatives qui peuvent aussi avoir beaucoup de modalités.  Et au delà même, pourquoi ne pas étendre ces questions également à la variable cible (à prédire) qui peut être de toutes nature ? 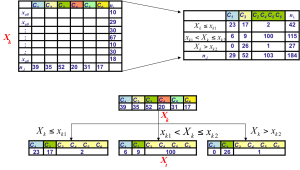 Ce travail nous a conduit à proposer une forme généralisée du partitionnement récursif. Nous avons ainsi abouti à un cadre générique qui permet de construire des graphes d’induction dans un contexte supervisé ou non supervisé, et cela, quel que soit le type et le nombre de variables prédictives ou à prédire. Il s’agit d’une généralisation des arbres de décision. Dernièrement, dans le cadre de la thèse de Vincent Pisetta, nous avons développé des travaux visant à utiliser les forêts aléatoires pour construire des fonctions Noyau conduisant à des classifieurs plus performants que les SVM.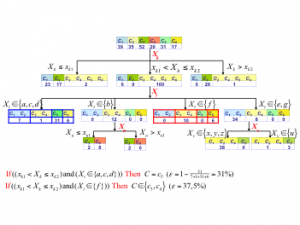

Graphes topologiques et apprentissage

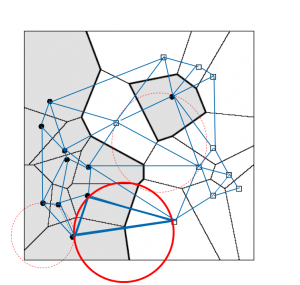
• Parmi les « classifieurs » les plus connus, les « k-plus proches voisins » (kppv) occupent une bonne place. Or, la relation binaire de voisinage, induite par les kppv, n’est pas symétrique, d’où un graphe non connexe. Pour cette raison et bien d’autres que je laisse de côté par manque de place, il nous a paru intéressant de rechercher des structures plus adaptées. Pour cela, nous avons fait appel aux modèles géométriques comme les polyèdres de Delaunay, les graphes de Gabriel ou des voisins relatifs qui rendent mieux compte de la topologie des points de l’ensemble d’apprentissage et qui produisent des graphes connexes où la relation de voisinage est toujours symétrique. Partant de là, nous avons pu répondre à un problème clé en apprentissage, à savoir la séparabilité des classes. En effet, si les classes étaient distribuées aléatoirement dans l’espace de représentation, il ne servirait alors à rien de chercher un algorithme d’apprentissage, car le seul modèle qui serait induit serait soit trop spécifique à cause du sur-apprentissage ou pas meilleur qu’un oracle prédisant selon la probabilité a priori des classes. Par l’étude de la structure de ces graphes géométriques, et en nous inspirant des travaux de la statistique spatiale, comme les travaux de Cliff et Ord, nous avons pu établir la loi exacte des arêtes coupées en cas de distribution aléatoire des classes. Une arrête du graphe est coupée si elle relie deux points de classes différentes. Nous avons proposé un test statistique. Outre la réponse au problème de la séparabilité des classes, nous poursuivons ces travaux pour trouver les meilleures fonctions noyau, celles qui conduisent à une meilleure séparabilité des classes. Cette piste nous paraît particulièrement intéressante pour deux raisons :
  • Elle propose extension aux méthodes basées sur les SVM (Support Vector Machines) notamment à travers la construction de nouveaux types de fonction noyau
  • Elle débouche sur une nouvelle vision de l’apprentissage qui rend la structure topologique centrale dans tout algorithme d’apprentissage

La fouille de données complexes

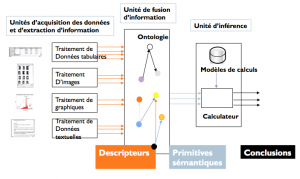Les techniques de fouille de données, dont l’objectif est d’exploiter des données massives en vue d’extraire des connaissances ou des informations utiles pour l’usager, sont bien adaptées pour traiter des données tabulaires décrites par des couples « attribut-valeur ». Or, les données accessibles dans ce format ne représentent qu’une faible part, située entre 10% et 15%, des données numérisées. Les vrais défis scientifiques et technologiques se situent dans la Fouille des Données Complexes comme celles qui sont sur le web par exemple (textes, images, vidéos). Ces données complexes se prêtent moins facilement à la fouille et par conséquent, nécessitent des approches et des outils nouveaux. C’est dans cette optique que, dès le début des années 2000, j’ai engagé des travaux autour de cette problématique où j’ai exploré deux voies :

– Recherche par le contenu dans les données complexes (Recherche d’Information (RI), Organisation et Indexation). 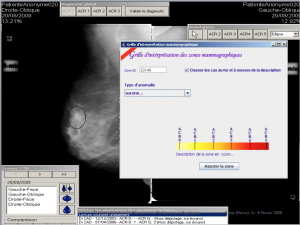 Il s’agit de trouver des modes de représentation pour les données complexes afin de pouvoir les interroger et de naviguer à l’intérieur. Le fait de recourir à des graphes géométriques offre, une fois le graphe construit, un fort potentiel en termes de navigation et de recherche d’information. – Prise en compte des connaissances du domaine dans la fouille de données complexes : 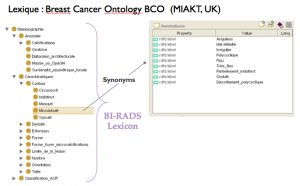Dans les premiers travaux, nous nous sommes vite aperçus que la fouille de corpus complexes pouvait être améliorée par la prise en compte d’informations externes. Cette idée a été exploitée pour déboucher sur des stratégies de prise en compte des connaissances du domaine par le biais des ontologies.

Développement de logiciels

Depuis le début de ma carrière universitaire, j’ai choisi de diffuser librement mes logiciels. Nous avons été parmi les premiers au monde (1995) à mettre un logiciel de fouille de données sur Internet en téléchargement libre. SIPINA, qui est un logiciel de fouille de données par les graphes d’induction. Il a, depuis, connu de nombreuses versions et il a été repris complètement au sein de la plate forme Tanagra par un chercheur de mon laboratoire. Tanagra[1]est maintenant un des logiciels phare du domaine.

Travaux appliqués

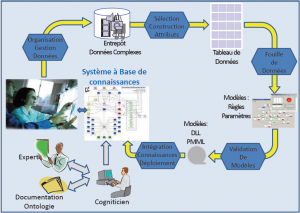Dans le cadre de contrats ou de collaborations ponctuelles, j’ai conduit de nombreuses recherches appliquées essentiellement dans deux secteurs :

• La santé, dans le cadre de la fouille de données complexes et son application pour l’aide au diagnostic dans les cancers du sein avec le Centre Léon Bérard de Lyon, le Centre d’Imagerie Médicale de Clermont-Ferrand, la société Fenics sas. Je coordonne actuellement un projet européen « FLURESP » destiné à modéliser les phénomènes de pandémie grippales. Ce projet bénéficie d’un financement européen (DG SANCO) global de 700 000 euro et implique 8 équipes européennes.
• Les sciences humaines et sociales à travers de nombreuses collaborations sur des applications touchant notamment la fouille de texte avec notamment l’Institut des Sciences de l’Homme de Lyon. En ce moment, nous travaillons sur la fouille d’opinion et les réseaux sociaux comme tweeter.